Resolución Final - Final A (2025) - Física 03 CBC Cátedra Única

Volver a Final

FÍSICA 03 CBC

CÁTEDRA ÚNICA

Final A (2025)

Ejercicio 1:

En un tubo en U como el de la figura, se colocan dos líquidos inmiscibles de densidades $\rho_1 = 1.2 \text{ g/cm}^3$ y $\rho_2 = 2.6 \text{ g/cm}^3$. Cuando se alcanza el equilibrio, la superficie libre del líquido 1 se halla por encima de la superficie libre del líquido 2. Considere que la altura de la columna del líquido 1 es de $l_1 = 80 \text{ cm}$

(a) Si ambas ramas se encuentran abiertas al aire, donde la presión es la atmosférica normal $(101300 \text{ Pa})$, calcule la diferencia de alturas $h$ entre los puntos $A$ y $B$

$\square$ $75 \text{ cm}$ $\square$ $43 \text{ cm}$ $\square$ $55 \text{ cm}$ $\square$ $47 \text{ cm}$ $\square$ $63 \text{ cm}$ $\square$ $34 \text{ cm}$

(b) Ahora considere que la rama izquierda sigue abierta a la atmósfera, ¿qué presión absoluta debería haber sobre la superficie del líquido 2 para que los puntos $A$ y $B$ se encuentren a la misma altura?

$\square$ $101300 \text{ Pa}$ $\square$ $95340 \text{ Pa}$ $\square$ $104380 \text{ Pa}$ $\square$ $70450 \text{ Pa}$ $\square$ $70849 \text{ Pa}$ $\square$ $90100 \text{ Pa}$

Ejercicio 2:

Un bote navega en línea recta entre los embarcaderos $A$ y $B$, ubicados en la misma orilla de un río y separados por una distancia de $120 \text{ m}$. La velocidad del bote con respecto al agua tiene una magnitud de $5 \text{ m/s}$ y la velocidad del agua respecto a la orilla de $3 \text{ m/s}$. Si la corriente del río fluye de $A$ hacia $B$ y el bote vuelve instantáneamente al llegar a $B$, ¿cuánto tiempo tarda en completar el recorrido de ida y vuelta?

$\square$ $75 \text{ s}$ $\square$ $64 \text{ s}$ $\square$ $80 \text{ s}$ $\square$ $120 \text{ s}$ $\square$ $30 \text{ s}$ $\square$ $48 \text{ s}$

Ejercicio 3:

Un paquete es lanzado desde una ventana a $h = 9 \text{ m}$ de altura por encima del suelo. Luego de recorrer una trayectoria parabólica cae al suelo a los $3$ segundos de haber sido lanzado y a una distancia horizontal de $21$ metros.

(a) ¿Cuál es el vector velocidad inicial $\vec{V_0}$ del paquete? (i y j son los versores que apuntan en las direcciones $x$ e $y$ respectivamente)

$\square$ $3 \text{ m/s } \hat{i} + 7 \text{ m/s } \hat{j}$ $\square$ $16 \text{ m/s } \hat{i} - 5 \text{ m/s } \hat{j}$ $\square$ $7 \text{ m/s } \hat{i} + 3 \text{ m/s } \hat{j}$

$\square$ $8 \text{ m/s } \hat{i} + 3 \text{ m/s } \hat{j}$ $\square$ $7 \text{ m/s } \hat{i} + 12 \text{ m/s } \hat{j}$ $\square$ $3 \text{ m/s } \hat{i} - 6 \text{ m/s } \hat{j}$

(b) Calcule la altura máxima alcanzada por el paquete respecto al suelo

$\square$ $16.2 \text{ m}$ $\square$ $9 \text{ m}$ $\square$ $20 \text{ m}$ $\square$ $14 \text{ m}$ $\square$ $32.1 \text{ m}$ $\square$ $38.3 \text{ m}$

Ejercicio 4:

Considere un cuerpo cúbico de lado $L$. Si se cuelga del techo mediante una soga ideal, la tensión que le ejerce la soga es igual a $220 \text{ N}$. Cuando el cuerpo está sumergido totalmente en agua $(\delta_{agua} = 1 \text{ kg/litro})$, la tensión que ejerce la soga es igual a $160 \text{ N}$. Entonces, el valor de $L$ es:

$\square$ $30 \text{ cm}$ $\square$ $5 \text{ cm}$ $\square$ $26 \text{ cm}$ $\square$ $35 \text{ cm}$ $\square$ $18 \text{ cm}$ $\square$ $45 \text{ cm}$

Ejercicio 5:

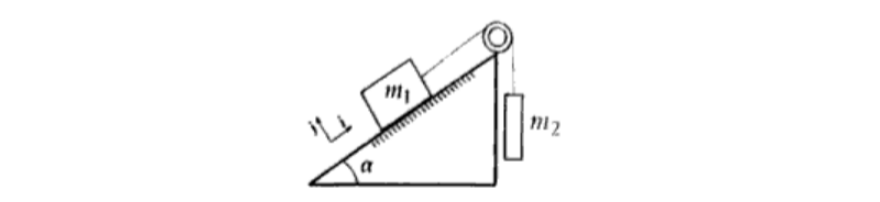
Se deja en libertad desde el reposo a dos cuerpos que están unidos por una cuerda ideal como muestra la figura. Considere que la masa del cuerpo $1$ es $m_1 = 6 \text{ kg}$, el ángulo del plano inclinado es $\alpha = 60°$ y que los coeficientes de rozamiento estático y dinámico entre $m_1$ y el plano son $\mu_e = 0.5$ y $\mu_d = 0.2$, respectivamente. Entonces,

(a) El mínimo valor de $m_2$ para que el sistema permanezca en reposo es aproximadamente:

$\square$ $1.7 \text{ kg}$ $\square$ $3 \text{ kg}$ $\square$ $2 \text{ kg}$ $\square$ $2.6 \text{ kg}$ $\square$ $3.7 \text{ kg}$ $\square$ $5.3 \text{ kg}$

(b) Si $m_2 = 2 \text{ kg}$, entonces luego de liberar a los cuerpos, la aceleración de $m_1$ de acuerdo al sistema de referencia de la figura es aproximadamente:

$\square$ $-3.3 \text{ m/s}^2 \, \hat{i}$ $\square$ $1.6 \text{ m/s}^2 \, \hat{i}$ $\square$ $-2.8 \text{ m/s}^2 \, \hat{i}$ $\square$ $0 \text{ m/s}^2 \, \hat{i}$ $\square$ $-1.2 \text{ m/s}^2 \, \hat{i}$ $\square$ $2.2 \text{ m/s}^2 \, \hat{i}$

Ejercicio 6:

Un cuerpo de masa $4 \text{ kg}$ se encuentra inicialmente en reposo comprimiendo a un resorte de constante elástica $3200 \text{ N/m}$ (ver figura). En cierto instante se lo deja en libertad, luego atraviesa un tramo de longitud $d = 2 \text{ m}$, que es el único con rozamiento de coeficiente dinámico $\mu_d = 0.2$, y pasa por el punto $A$ con una velocidad de módulo $5 \text{ m/s}$. Posteriormente, sube sin despegarse del piso, y finalmente pasa por el punto $C$ que se encuentra a una altura $h = 1 \text{ m}$ respecto al piso. Determine:

(a) La compresión inicial del resorte:

$\square$ $10 \text{ cm}$ $\square$ $16 \text{ cm}$ $\square$ $31 \text{ cm}$ $\square$ $4 \text{ cm}$ $\square$ $6 \text{ cm}$ $\square$ $20 \text{ cm}$

(b) La variación de energía cinética del cuerpo al desplazarse desde el punto $B$ al punto $C$

$\square$ $40 \text{ J}$ $\square$ $16 \text{ J}$ $\square$ $-80 \text{ J}$ $\square$ $-16 \text{ J}$ $\square$ $-40 \text{ J}$ $\square$ $80 \text{ J}$

Ejercicio 7:

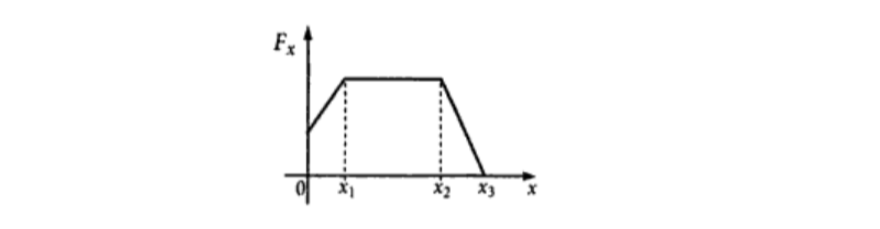
Un objeto que se encuentra inicialmente en reposo es sometido a una fuerza resultante en la dirección del eje $x$. La fuerza varía con la posición como muestra la figura. Cuando el objeto se desplaza en sentido positivo se verifica que:

$\square$ Entre las posiciones $x_2$ y $x_3$ su velocidad disminuye

$\square$ En la posición $x_3$ su velocidad es cero

$\square$ En la posición $x_1$ alcanza su velocidad máxima

$\square$ Entre las posiciones $x_1$ y $x_2$ su velocidad es constante

$\square$ Su velocidad en la posición $x_1$ es mayor que en $x_3$

$\square$ Entre las posiciones $x_1$ y $x_2$ su velocidad aumenta

Ejercicio 8:

Un satélite de masa $M$ describe un movimiento circular uniforme a una altura $h = R_T$ (sobre la superficie de la Tierra) ¿Cuál de las siguientes afirmaciones es la única verdadera?

Datos: Radio terrestre $R_T = 6370 \text{ km}$, $G = 6.67 \cdot 10^{-11} \text{ Nm}^2 \text{/kg}^2$, masa terrestre $M_T = 6 \cdot 10^{24} \text{ kg}$, y $g$ es la aceleración de la gravedad en la superficie terrestre.

$\square$ La fuerza gravitatoria sobre el satélite es $M \cdot g$

$\square$ La aceleración del satélite es $g/4$

$\square$ Como el satélite describe un movimiento circular uniforme, entonces su aceleración es $0$

$\square$ La fuerza que la Tierra ejerce sobre el satélite es mucho mayor que la que el satélite ejerce sobre la Tierra

$\square$ La aceleración del satélite a esa altura es $g/2$

$\square$ La fuerza gravitatoria sobre el satélite es $2 \cdot M \cdot g$

CURSO RELACIONADO

Física 03

2025 ÚNICA

¿Te ayudan nuestros exámenes?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰

Ir al curso

¿Listx para rendir?

Elegí la modalidad y empezá 👉

Interactivo Simulacro